Valentine, Tom --- "Uncovered Share Return Parity for Australian Shares" [2006] JlLawFinMgmt 4; (2006) 5(1) Journal of Law and Financial Management 40

• Abstract
• 1. Introduction
• 2. Share Return Parity
• 3. The International CAPM
• 4. Implications
• References

---

Uncovered Share Return Parity for Australian Shares

Tom Valentine
University of Western Sydney

Abstract

Interest rate parity (both covered and uncovered) is a well-established relationship in international finance. This theory has led by analogy to the suggestion that an equivalent relationship would exist for share returns.

This paper explores such a share return parity relationship for the Australian and US share markets. An initial estimation suggests that Australian share returns do not fully reflect movements in US share returns. There are a number of explanations for this result. First, since market participants must react to expected returns, the expectations generating mechanisms (including that for changes in exchange rates) used in Australia and the United States may differ.

Secondly, Australian and US shares may not be perfect substitutes. In particular, they may be perceived to have different risk characteristics. When this possibility is taken into account, a good explanation is obtained. The results throw some light on the desirability of offshore investment for Australian investors. However, the problem of proxying for expectations remains.

1. Introduction

Financial deregulation has increased the integration of global financial markets and this development has a number of important implications. For example, it affects the extent to which foreign factors influence Australian financial markets and in particular the cost of capital for Australian businesses. It is also relevant to determining the channels through which monetary policy affects the Australian economy. In addition, it affects the decisions of Australians as to the extent to which they invest offshore.

The purpose of the present study is to examine the degree of integration of Australian financial markets with overseas financial markets in the context of share investments. The second section of the paper considers integration in terms of share return parity. This relationship will be established only under certain strict assumptions and an empirical test of it is actually a test of the joint hypothesis that the assumptions of the model are correct. The empirical results presented in this section suggest that the theory is not completely satisfactory.

The third section of the paper considers an alternative version of the share return parity relationship which is based on the international capital asset pricing model (CAPM). This model gives superior results and the fourth section considers their implications.

2. Share Return Parity

There are a number of approaches to measuring the degree of integration of financial sectors in different countries and they are surveyed in Adam et. al. (2002). This paper is concerned with the integration of investment markets and two alternative approaches are worth considering.

The first is to consider whether there are any impediments to investment flows leaving or entering the country. In the case of Australia it can be noted:

• there are no significant controls preventing Australian residents from investing offshore or offshore investors from investing in Australian based assets. The only minor exception is the restrictions on overseas ownership exercised by the Treasurer and the Foreign Investment Review Board (FIRB);

• information on global markets is fully and rapidly distributed to Australian investors and overseas investors are fully informed on developments in Australian markets; and

• many Australian companies are multinational corporations with extensive offshore activities and this will contribute to the integration of global markets. For example, multinational corporations will obtain their funding and make their financial investments in any market that appears to offer more attractive opportunities than others.

A second approach is to test the implications of complete integration. An important implication of fully capital mobility is that parity relationships will be established for the same assets in different markets. Note that for a parity relationship to be established, the assets considered must be perfect substitutes.

The best known parity relationship is uncovered interest rate parity. Consider the case of Australians investing in US fixed interest securities and vice-versa. The relationship is:

Note that equation (1) is an approximation and that the exchange rate is stated in direct terms rather than the indirect form used in the Australian market. This is the case throughout the paper.

The right-hand side of equation (1) is the expected return to an Australian resident investing in US bonds. If this is higher than the return to investing in equivalent Australian bonds (ra), funds will flow out of Australia and into US bonds. This outflow could cause an increase in the yield on Australian bonds, but the most likely adjustment is a depreciation of the Australian dollar which will reduce e*.

One difficulty in empirical tests of equation (1) is that the return to investing in US bonds is uncertain and, therefore, investors will demand a risk premium for investing in that way. That is, the right-hand equation should include a risk premium and it is realistic to assume that this risk premium varies over time.

A second difficulty is that in order to implement equation (1) it is necessary to specify the mechanism generating e*. Therefore, any empirical test of equation (1) is a test of the joint hypothesis that

• uncovered interest rate parity applies;

• exchange rate expectations are generated by the assumed mechanism; and

• the risk premium is generated by the assumed mechanism.

In the case of the third hypothesis the mechanism assumed is often that the risk premium is zero or is a random variable uncorrelated with the other regressors.

An additional problem in testing relationship (1) is that it assumes that investors perceive Australian and US bonds as perfect substitutes. All of these problems may explain the results discussed by Gruen and Menzies (1991) which give limited support to uncovered interest rate parity. It should be noted, however, that the Gruen and Menzies (1991) assume rational expectations as the expectations generating mechanism. That is, they test whether the interest rate differential correctly forecasts the actual change in the exchange rate.

Uncovered share return parity can be postulated by analogy with uncovered interest rate parity. Again using the US as an example the equation is:

The following two equations are empirical versions of equation (2). The dependent variable (sa) is the return on the ASX/SP200. The first independent variable (sdj) is the return on the Dow Jones index. The expected change in the exchange rate is based on the assumption of static expectations.

where e is the Australian dollar/US dollar exchange rate in direct form.

The equation has been estimated from quarterly data for the period 1994(3) to 2004(2). The figures under the coefficients are t-statistics and asterisks indicate the degree of significance. One asterisk means the coefficient is significant at the five percent level and two asterisks indicate significance at the one percent level. Standard errors have been estimated using the White heteroscedasticity-consistent estimator. 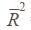is the adjusted coefficient of determination and d is the Durbin-Watson statistic.

In estimating equations such as (4), it is necessary to ensure that there is no unit root in the process generating the data. If such a root is present, spurious results can be obtained. In the present study this possibility is tested by testing for the presence of a unit root in the regression residuals using the tables given by Davidson and Mackinnon (1993), Table 20.2. The hypothesis that there is a unit root in the errors in equation (4) is rejected.

The stability of the equation has been tested using the CUSUM of squares test. There is no evidence of instability.

The following equation relates the return on Australian shares to the return on the MSCI (sm) and the percentage change in the TWI for the Australian dollar (et).

The residuals from this equation show no evidence of the presence of a unit root and there is no evidence of coefficient instability.

Equations (4) and (5) provide strong evidence of a relationship between the return on Australian shares and the return on overseas shares, providing support for the view that the Australian sharemarket is highly integrated with overseas sharemarkets. However, the equations do not fully support share return parity because in both equations the coefficients of the overseas returns are significantly less than unity. This outcome differs from the result obtained by Valentine (2000, p. 190) for the period 1984 (3) – 1997 (4) using EGARCH (exponential generalised autoregressive conditional heteroscedasticity) estimation. The approach is based on the insight that in financial relationships, large disturbances tend to be concentrated in successive time periods. As a first step equations (4) and (5) were re-estimated using the GARCH (1,1) model (see Alexander and Riyait (1992)), but the coefficients in this model are all insignificant. Also, there is no change in the estimated beta. The equations were then re-estimated using EGARCH (Nelson (1991)). However, the results of this estimation were the same as those produced by the GARCH model.

3. The International CAPM

Sercu and Uppal (1995, ch. 22) consider the international CAPM and their analysis produces the equation (using the US as an example):

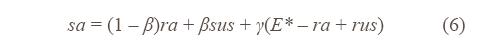
In this equation ra and rus are risk-free rates. This equation does not assume that Australian and overseas shares are perfect substitutes because the coefficient β measures the relationship between the return on Australian shares and the return on overseas shares. This equation generalises the traditional CAPM by including two sources of systematic risk – market variability and exchange rate variability. The third term is the return to an Australian resident holding US dollars multiplied by γ which indicates the relationship between that return and the return on Australian shares. It is

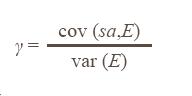
According to the assumptions of CAPM, the remaining variability is random (that is, it represents the diversifiable risk). The third regressor in the equation 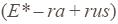derives from the uncertainty about the exchange rate. Therefore, there is no reason to add a risk premium to equation (6).

Estimation of equation (6) requires that a restriction be applied to the coefficients of ra and sus.

The first estimate of equation (6) produced the following results. Once again sdj is used for sus and e* is proxied by e_-1. The 90 day bill rate is used for ra and the three month Treasury bill rate is used for rus. The coefficient α is the constant in the equation.

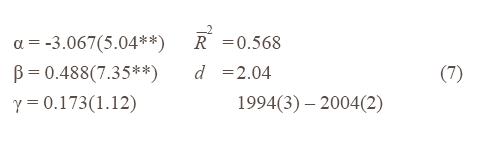
The hypothesis that the residuals contain a unit root is rejected and a CUSUM of SQUARES test of the unrestricted version of the equation shows no evidence of coefficient instability. A Wald test of the restriction on the coefficients of ra and sdj accepts it.

The second version of equation (6) is based on the assumption that the MSCI represents the global market. sm is the return on the MSCI. e* is proxied by et_-1 and rus is used as a proxy for the global risk-free rate.

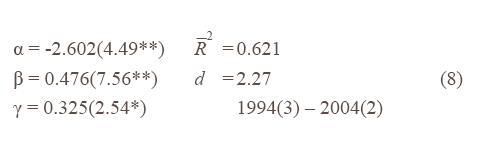
There is no evidence of a unit root in the residuals and the unrestricted version of the equation shows no sign of coefficient instability. The restriction on the coefficients of ra and sm is accepted.

Also, there is no sign of autocorrelation in the disturbances of the equation. All of these results suggest that this equation does not require a risk premium, providing some further support for the international CAPM.

4. Implications

Equation (8) indicates that the Australian share market is highly integrated with overseas share markets. The average return on Australian shares is determined by the return on overseas shares and a factor arising from uncertainty about exchange rates.

The results provide support for the international CAPM. They also suggest that using the domestic CAPM is likely to give poor results because the definition of the “market” that it uses is too restrictive. The equation allows us to consider the effect of changes in monetary policy, as reflected in changes in the risk-free rate, on the cost of capital in Australia. The coefficient of ra in equation (8) is 0.199. This result suggests that a tightening of monetary policy does not have a major impact on the cost of capital for Australian businesses. It is therefore unlikely to have a major impact on business investment.

The equation also shows that the Australian share market is low risk relative to overseas markets. It has a beta which is less than 0.5. This result indicates that Australian shares are far from being perfect substitutes for overseas shares. This outcome provides an argument for Australian investors who are very risk averse to remain onshore although they are frequently urged not to do so. It also indicates that a well diversified share portfolio is likely to have a significant representation of Australian shares. It should be noted that the betas for some individual shares relative to the global market will be well above unity and these shares may not be attractive to risk averse investors.

References

Adam, K., T. Jappelli, A. Menichini, M. Padula and M. Pagano (2002), "Analyse, Compare, and Apply Alternative Indicators and Monitoring Methodologies to Measure the Evolution of Capital Market Integration in the European Union", Centre for Studies in Economics and Finance, University of Salemo, January.

Alexander, C. and Riyait, N. (1992), “The World According to GARCH”, Risk, vol.5, September, pp.120-125.

Davidson, R. and J. Mackinnon (1993), Estimation and Inference in Econometrics, (Oxford University Press; New York).

Gruen, D.W.R. and G.D. Menzies, "The Failure of Uncovered Interest Parity: Is It Near - Rationality in the Foreign Exchange Market", Research Discussion Paper 9103, Research Department, Reserve Bank of Australia.

Nelson, D.B. (1991), “Conditional Heteroscedasticity in Asset Returns: A New Approach”, Econometrica, vol.59, pp.347-70.

Sercu, P. and R. Uppal (1995), International Financial Markets and the Firm, (Chapman and Hall, Cincinnati).

Valentine, T. (2000), "Share Prices and Fundamentals" in P. Abelson and R. Joyeux (editors), Economic Forecasting, (Allen and Unwin, Sydney).